ある事柄の起こり方が何通りあるか数えたものを, 場合の数といいます.
その代表例, 順列と組合せについて解説します.
■順列 って?■
ある \(5\) 人組アイドルグループのメンバー
A (歌唱力抜群), B (顔面偏差値95), C (神トーク), D (お笑い担当), E (塩対応)
のうち \(3\) 人が, \(1\) 人ずつ歌手としてソロデビューしていく.
例えば, A→B→E の順でデビュー.
このように, いくつかのものから順序をつけて選んだものが 順列 (Permutation) だ. そこでは,
順序が違えば別ものと考える.
実際, A→B→E ではなく B→E→A だと, なんで歌の上手い A は後のほうなんだとファンは騒ぐんじゃないか?
A→B→E と B→E→A は, メンバーは同じだが順序が違うので区別され, 異なる \(2\) 通りと数えるんだ.
では, この順列は全部で何通りあるかな? 樹形図 を書くとよくわかる.
まず, \(1\) 番目のデビューがだれかで \(5\) 通り. \(5\) 本の枝が生じる.
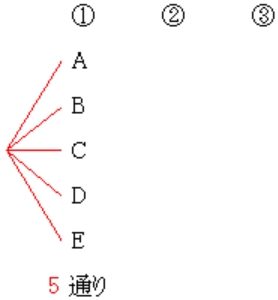
例えば \(1\) 番目が A のとき, \(2\) 番目は A 以外の \(4\) 通り.
\(1\) 番目が A でないときも同様.
全体として枝の本数が \(4\) 倍に増殖する.
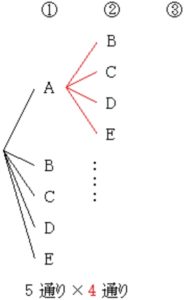
例えば \(1\) 番目が A で \(2\) 番目が B のとき, \(3\) 番目は A と B 以外の \(3\) 通り.
他の場合も同様.
全体として枝の本数がさらに \(3\) 倍に増殖する.
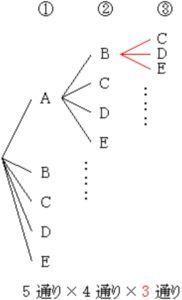
最終段階 ③ の枝の総数
\(5\times4\times3(={}_{5}\)\(\rm{P}\)\(_{3})=60\)
が, 求める順列の総数だ.
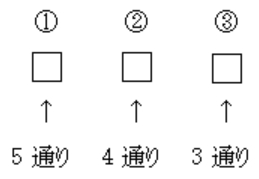
しかし樹形図を毎回書くのは疲れるので, 代わりに, 次のように
箱 (□) の中に文字を入れていく方法が何通りあるかを数える
のがよい.
●例題 1 <順列>●
A, B, C, D, E の \(5\) 人から \(3\) 人を選んで \(1\) 列に並べる方法は何通りあるか.
●解答●
\(({}_{5}\)\(\rm{P}\)\(_{3}=)5\times4\times3=60\ [通り]\)
答 \(60\) 通り
異なる \(5\) 個のものから \(3\) 個をとる順列の総数を \({}_{5}\)\(\rm{P}\)\(_{3}\) で表し, 一般に,
\({}_{n}\)\(\rm{P}\)\(_{r}=n(n-1)(n-2)\cdots(n-r+1)\)
となるのですが, このような 「呪文」 をただ覚えることに何の意味もありません.
樹形図について理解しているならば, その呪文はもう必要ないでしょう.
理解は暗記を減らします.
★Point 1 <順列>★
箱 (□) の中に文字を入れていく方法が何通りあるかを数える.
(樹形図 の枝数のかけ算をイメージ)
SPONSORED LINK
■組合せ って?■
ある \(5\) 人組アイドルグループのメンバー
A (歌唱力抜群), B (顔面偏差値95), C (神トーク), D (お笑い担当), E (塩対応)
のうち \(3\) 人が組んで新しいユニットとしてデビューする.
例えば, A-B-E の組でデビュー.
このように, いくつかのものから選んだだけものが 組合せ (Combination) だ. そこでは,
順序が違っても同じものと考える.
実際,
「A と B と E がユニットデビューするんだって!」
と言うのと,
「B と E と A がユニットデビューするんだって!」
と言うのは同じことで,
「どっちなんだよwwwww」
とネットに書き込むファンはまずいない. ライブへ行く前に病院だ.
順序は違ってもメンバー構成は同じだから区別されず, 同じ \(1\) 通り A-B-E と考えるんだ.
\(6\) 通りの順列
A→B→E
A→E→B
B→A→E
B→E→A
E→A→B
E→B→A
は全部, 組合せとしては \(1\) 通りとされる.
ちなみに \(6\) 通りというのは,
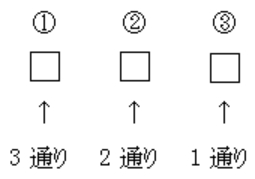
\(3\times2\times1(={}_{3}\)\(\rm{P}\)\(_{3})\) の計算結果ね.
では, ユニット (組合せ) の総数 (\(x\) 通りとしよう) を計算で求めるにはどうしたらいいかな?
その方法はなんと…
ソロデビューの場合の数から逆算するのだ!
先に述べた, \(5\) 人から \(3\) 人を選んで \(1\) 人ずつソロデビューさせるというのは,
① まず \(5\) 人から \(3\) 人を選んでユニットをつくり,
② その \(3\) 人を順にソロデビューさせる
という \(2\) 段階を踏んでも結果的には同じことだ.
① は \(x\) 通りで, そのそれぞれについて ② は \(6(=3\times2\times1)\) 通りだから, 全部で
\(x\times6\ [通り]\)
これは先に計算した
\(60(=5\times4\times3)\ [通り]\)
と一致するはずだから,
\(x\times6=60\)
より,
\(x=\displaystyle\frac{60}{6} \left(=\frac{5\times4\times3}{3\times2\times1} \right)\)
を計算すれば求まる.
●例題 2 <組合せ>●
A, B, C, D, E の \(5\) 人から \(3\) 人を選ぶ方法は何通りあるか.
●解答●
\(({}_{5}\)\(\rm{C}\)\(\displaystyle_{3}=)\frac{5\times4\times3}{3\times2\times1}=\frac{60}{6}=10\ [通り]\)
答 \(10\) 通り
異なる \(5\) 個のものから \(3\) 個をとる組合せの総数を \({}_{5}\)\(\rm{C}\)\(_{3}\) で表し,
\({}_{5}\)\(\rm{C}\)\(\displaystyle_{3}=\frac{5\times4\times3}{3\times2\times1}=\frac{{}_{5}{P}_{3}}{{}_{3}P_{3}}\)
一般に,
\({}_{n}\)\(\rm{C}\)\(\displaystyle_{r}=\frac{n(n-1)(n-2)\cdots(n-r+1)}{r(r-1)(r-2)\cdots3\times2\times1}=\frac{{}_{n}P_{r}}{{}_{r}P_{r}}\)
となりますが, この式を覚えるというよりは, 先に述べた原理をしっかり理解して, 公式を忘れてもその場で導けるようにしておきましょう.
それが無敵の学習法なのです.
ここでは場合の数の代表例である順列と組合せについて説明しましたが, それが場合の数のすべてではありません.
\({}_{n}\)\(\rm{P}\)\(_{r}\) とか \({}_{n}\)\(\rm{C}_{r}\) だけすべての問題が解けると思い込んでいる人は, ずっと場合の数が得意になれません.
「日本地図を, 隣り合う都道府県を別色にして \(4\) 色で塗り分ける方法」 なんて P と C だけでは難しいでしょう.