■関数とそのグラフ■
\(1\) を入れたら \(3\) を出す
\(2\) を入れたら \(5\) を出す
\(3\) を入れたら \(7\) を出す
\(\cdots\)
というように
「入れた数を \(2\) 倍して \(1\) を加えて出す」
という 「機能 (function)」 をもった 「はこ (函)」 があるとしよう.
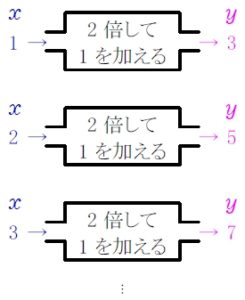
入れる数を \(x\), 出す数を \(y\) と名付けると,
\(1\) つの \(x\) を入れたとき, 出てくる \(y\) は必ず \(1\) つだ.
\(y\) が \(2\) つも \(3\) つも出てくることはないよね.
このように, \(1\) つの \(x\) に対して \(1\) つの \(y\) が決まるとき,
「\(y\) は \(x\) の \(\large{関数}\) (function) である」 というんだ.
そしてそれは, 「\(1\) つ入れたら \(1\) つ出す はこ (函)」 に例えられる.
実際, 昔は 「関数」 を 「函数」 と書いたらしい (読み方は同じ) .
“function” の中国語の音訳が 「函数 (hánshù)」 なんだとか.
さて, 先の 「はこ」 の機能からすると
「\(y\) は \(x\) の \(2\) 倍に \(1\) を加えたもの」
だから
\(\color{magenta}{y}=2\color{royalblue}{x}+1\)
と表されるね.
\(\color{magenta}{y}=2\color{royalblue}{x}+1\) という 「はこ」 の, 入れる数と出す数の一覧表をつくってみよう.
\begin{array}{c||c|c|c|c|c|c|c}
\color{royalblue}{x} & \cdots & \color{royalblue}{1} & \cdots & \color{royalblue}{2} & \cdots & \color{royalblue}{3} & \cdots \\ \hline
\color{magenta}{y} & \cdots & \color{magenta}{3} & \cdots & \color{magenta}{5} & \cdots & \color{magenta}{7} & \cdots \\
\end{array}
見ての通り 「書ききれない」.
大きい数や小さい数はもちろん,
\(x=1\) と \(x=2\) の間の小数や分数や \(\sqrt{2}\ (=1.4142\cdots)\) なんかを書き出すときりがない.
これを解決したのが, 関数の \(\large{グラフ}\) だ.
直交させた \(2\) つの数直線 (\(\large{x\ 軸}\) と \(\large{y\ 軸}\)) からなる平面 (\(\large{座標平面}\)) 上に値の組を点として表す.
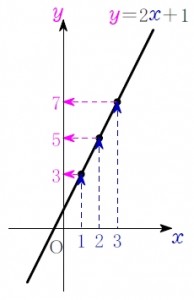
\(1\) つの \(x\) を入れたら \(1\) つの \(y\) を出す機能がよく表れているし,
グラフの連続性により \(x=1\) と \(x=2\) の間の無数の値についても表現できているね.
そして,
グラフは無数の点 \((x,\ y)\) の集まり
この意識はとても大事だ.
★Point 1 <関数とグラフ>★
\(\large{関数}\) \(\cdots\) \(1\) つの値に対して \(1\) つの値が決まる対応規則.
関数のグラフは無数の点の集まり.
■ 1 次関数とそのグラフ■
\(\large{y=ax+b}\) \((a\not=0)\) で表される関数を \(\large{1\ 次関数}\) という.
\(1\) 次関数のグラフの性質を調べよう.
それが分かれば 「この関数のグラフをかけ」 とか, 「グラフの式を求めよ」 とか言われても答えられるでしょ.
\(y=2x+1\) のグラフでは,
\(x\) の値が \(1\) 増えると \(y\) の値は \(2\) 増える.
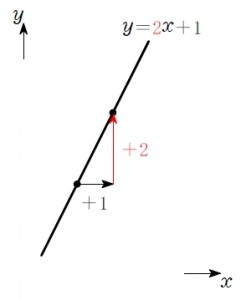
これがどこでも成り立つので, \(x\) の値に対して \(y\) の値は 「直線的に」 変化することがわかる.
そう, \(1\) 次関数の式を満たす点 \((x,\ y)\) の集まりは \(\large{直線}\) だ.
\(x\) の値が \(1\) 増えると \(y\) の値が \(2\) 増える直線は, 傾き \(2\) の直線というんだ.
この 「\(2\)」 は, \(y=\color{red}{2}x+1\) の \(x\) の係数になっているね.
直線上で, \(x\) 座標が \(1\) 増えたときの \(y\) 座標の変化量を \(\large{傾き}\) という.
直線 \(y=\color{red}{a}x+b\) の傾きは \(a\).
例えば \(x=5\) のときと \(x=6\) のときを比べてみると
\(x=5\) のとき \(y=a\times5+b=5a+b\)
\(x=6\) のとき \(y=a\times6+b=6a+b\)
\(x\) が \(1\) 増えると \(y\) は \(a\) だけ増えているので, たしかに傾きは \(a\) だね.
傾き \(a\) が正の数のときは, 直線は 「右上がり」 になる.
逆に, 傾き \(a\) が負の数のときは, 直線は 「右下がり」 になる.
例えば \(y=\color{red}{-3}x+2\) の傾きは \(-3\) で, \(x\) が \(1\) 増えると \(y\) は \(-3\) 増える (\(3\) 減る).
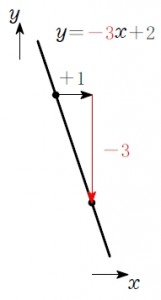
なお, 傾き \(a\) が \(0\) のときは, 「傾いていない」 わけだから, 水平線 (\(x\) 軸に平行) になる.
例えば \(y=1\) (\(y=\color{red}{0}x+1\)).
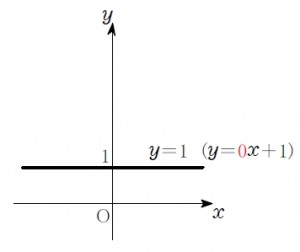
これは \(x\) の値が何であっても \(y\) の値は常に定数 \(1\) だ.
関数 \(y=b\ \ (定数)\) は \(1\) 次関数ではなく, 定数関数とよばれる.
さて, \(y=2x+1\) に話を戻そう.
これに \(x=0\) を代入すると,
\(y=2\times0+\color{red}{1}=\color{red}{1}\)
これは, \(y=2x+\color{red}{1}\) のグラフが \(y\) 軸上の \(y\) 座標 \(1\) の点を通ることを意味する.
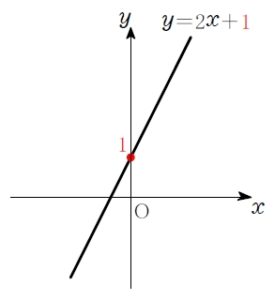
直線と \(y\) 軸との交点の \(y\) 座標を \(\large{y\ 切片}\) という.
直線 \(y=ax+\color{red}{b}\) の \(y\) 切片は \(b\).
\(b\) が \(0\) のときは \(y=ax\) \((a\not=0)\) となり,
「\(y\) は \(x\) に比例する」 といい, \(a\) を比例定数という.
比例の関数は \(1\) 次関数のなかまだ.
★Point 2 < 1 次関数>★
関数 \(\large{y=ax+b}\) \((a\not=0)\)
グラフは 傾き \(a\), \(y\) 切片 \(b\) の \(\large{直線}\).
\(a>0\) なら 右上がり
\(a<0\) なら 右下がり
■ 2 乗に比例する関数とそのグラフ■
\(\large{y=ax^2}\) \((a\not=0)\) のとき,
「\(y\) は \(x\) の\(2\) 乗に比例する」 という.
まずは \(a=2\) の場合 \(\color{magenta}{y}=2\color{royalblue}{x}^2\) ついて調べてみよう.
\begin{array}{c||c|c|c|c|c|c|c}
\color{royalblue}{x} & \cdots & \color{royalblue}{-2} & \cdots & \color{royalblue}{-1} & \cdots & \color{royalblue}{0} & \cdots & \color{royalblue}{1} & \cdots & \color{royalblue}{2} & \cdots \\ \hline
\color{magenta}{y} & \cdots & \color{magenta}{8} & \cdots & \color{magenta}{2} & \cdots & \color{magenta}{0} & \cdots & \color{magenta}{2} & \cdots & \color{magenta}{8} & \cdots \\
\end{array}
この式を満たす点 \((\color{royalblue}{x},\ \color{magenta}{y})\) の集まりは次のようになる.
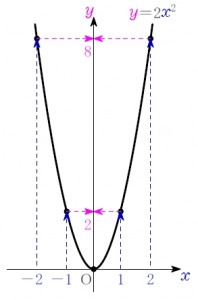
続いて \(a=-2\) の場合である \(\color{magenta}{y}=-2\color{royalblue}{x}^2\).
これは \(2x^2\) の逆符号なので
\begin{array}{c||c|c|c|c|c|c|c}
\color{royalblue}{x} & \cdots & \color{royalblue}{-2} & \cdots & \color{royalblue}{-1} & \cdots & \color{royalblue}{0} & \cdots & \color{royalblue}{1} & \cdots & \color{royalblue}{2} & \cdots \\ \hline
\color{magenta}{y} & \cdots & \color{magenta}{-8} & \cdots & \color{magenta}{-2} & \cdots & \color{magenta}{0} & \cdots & \color{magenta}{-2} & \cdots & \color{magenta}{-8} & \cdots \\
\end{array}
\(y=2x^2\) のグラフを上下にひっくり返した形になる.
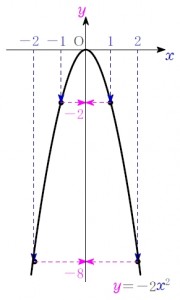
物体を斜め上に放り投げたときの, 物体が描く曲線に似ているね.
そう, \(y=ax^2\ \ (a\not=0)\) を満たす点 \((x,\ y)\) の集まりは, 原点 \(\rm{O}(0,\ 0)\) を頂点とする \(\large{放物線}\) だ.
\(a>0\) のときの形を \(\large{下に凸}\),
\(a<0\) のときの形を \(\large{上に凸}\) という.
■ 2 次関数とそのグラフ■
\(\large{y=ax^2+bx+c}\) \((a\not=0)\) で表される関数を \(\large{2\ 次関数}\) という.
\(b=0\), \(c=0\) のときは \(y=ax^2\) となる.
\(y=2(x-3)^2\) みたいな式も, 右辺を展開, 整理すると
\(y=2(x^2-6x+9)\)
\(=2x^2-12x+18\)
となって \(a=2\), \(b=-12\), \(c=18\) の場合だね.
\(y=2(x-3)^2\) と \(y=2x^2\) のグラフを比べてみよう.
\(y=2(x-3)^2\) に \(x=\color{red}{4}\) を代入してみると,
\(y=2(4-3)^2\)
\(=2\times1^2\)
これは \(y=2x^2\) に \(x=\color{red}{1}\) を代入したときの \(y\) の値になっている.
\(y=2x^2\) の \(x\) よりも \(3\) 大きい 値を \(y=2(x-3)^2\) に代入すると, 両者の \(y\) の値は等しくなる.
\begin{array}{c||c|c|c|c|c|c|c}
x & \cdots & -2 & \cdots & -1 & \cdots & 0 & \cdots & \color{red}{1} & \cdots & 2 & \cdots \\ \hline
2x^2 & \cdots & 8 & \cdots & 2 & \cdots & 0 & \cdots & \color{magenta}{2} & \cdots & 8 & \cdots \\
\end{array}
\begin{array}{c||c|c|c|c|c|c|c}
x & \cdots & 1 & \cdots & 2 & \cdots & 3 & \cdots & \color{red}{4} & \cdots & 5 & \cdots \\ \hline
2(x-3)^2 & \cdots & 8 & \cdots & 2 & \cdots & 0 & \cdots & \color{magenta}{2} & \cdots & 8 & \cdots \\
\end{array}
これにより, \(y=2(x-\color{red}{3})^2\) のグラフは放物線 \(y=2x^2\) を \(x\) 軸方向に \(3\) だけずらした位置にくる.
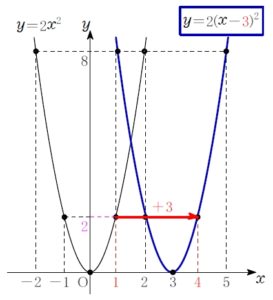
\(y=2(x-\color{red}{3})^2\) を満たす点 \((x,\ y)\) の集まりも放物線で, 頂点の座標は \((\color{red}{3},\ 0)\) になるとわかる.
\(y=a(x-\color{red}{p})^2\) のグラフは, \(y=ax^2\) のグラフを \(x\) 軸方向に \(p\) だけ平行移動したもので, 頂点は \((\color{red}{p},\ 0)\).
さらに, \(1\) つの \(x\) の値 (例えば \(x=\color{magenta}{4}\)) に対して, \(y=2(x-3)^2+1\) の \(y\) の値は, \(y=2(x-3)^2\) の \(y\) の値より \(1\) 大きい.
\begin{array}{c||c|c|c|c|c|c|c}
x & \cdots & 1 & \cdots & 2 & \cdots & 3 & \cdots & \color{magenta}{4} & \cdots & 5 & \cdots \\ \hline
2(x-3)^2 & \cdots & 8 & \cdots & 2 & \cdots & 0 & \cdots & \color{red}{2} & \cdots & 8 & \cdots \\
\end{array}
\begin{array}{c||c|c|c|c|c|c|c}
x & \cdots & 1 & \cdots & 2 & \cdots & 3 & \cdots & \color{magenta}{4} & \cdots & 5 & \cdots \\ \hline
2(x-3)^2+1 & \cdots & 9 & \cdots & 3 & \cdots & 1 & \cdots & \color{red}{3} & \cdots & 9 & \cdots \\
\end{array}
だから, \(y=2(x-3)^2+\color{red}{1}\) のグラフは放物線 \(y=2(x-3)^2\) を \(y\) 軸方向に \(1\) だけずらした位置にくる.
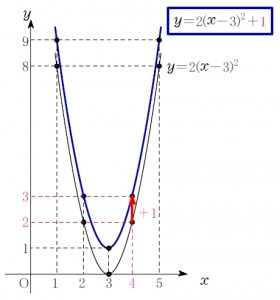
\(y=2(x-3)^2+\color{red}{1}\) を満たす点 \((x,\ y)\) の集まりも放物線で, 頂点の座標は \((3,\ \color{red}{1})\) になるとわかる.
\(y=a(x-p)^2+\color{red}{q}\) のグラフは, \(y=a(x-p)^2\) のグラフを \(y\) 軸方向に \(q\) だけ平行移動したもので, 頂点は \((p,\ \color{red}{q})\).
★Point 3 < 2 次関数>★
関数 \(\large{y=ax^2+bx+c}\) \((a\not=0)\)
\(\large{y=a(x-p)^2+q}\) とも表され,
グラフは頂点 \((p,\ q)\) の \(\large{放物線}\).
\(a>0\) なら 下に凸
\(a<0\) なら 上に凸
SPONSORED LINK
■グラフと領域■
\(y=2x+1\) のグラフとは, この方程式を満たす点 \((x,\ y)\) の集まりだったね.
だったら, 不等式 \(y>2x+1\) を満たす点 \((x,\ y)\) の集まりも, 当然あるんじゃないか.
\(y>2x+1\) にいろんな \(x\) の値を代入して考えてみよう.
\(x=1\) を代入すると \(y>3\) という式になる.
これは \(x\) 座標が \(1\) で, \(y\) 座標が \(3\) より大きい点すべてを表す.
例えば, 点 \((1,\ 4)\) とか点 \((1,\ 5)\) とかいっぱいある.
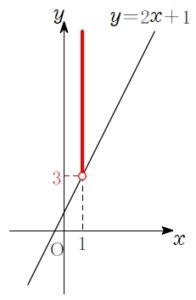
\(x=2\) のときは \(y>5\)
\(x=3\) のときは \(y>7\)
\(\cdots\)
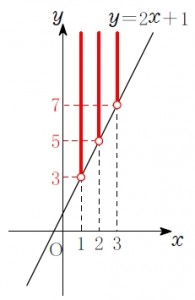
すべての \(x\) について, 不等式を満たす点 \((x,\ y)\) をとっていくと,
直線 \(y=2x+1\) より大きい \(y\) 座標をもつ点全体の集まりになる.
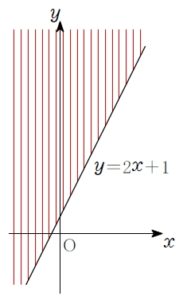
このように, 平面的な広がりをもった点の集まりを \(\large{領域}\) という.
つまり, 不等式 \(y\color{red}{>}2x+1\) の表す領域は, 直線 \(y=2x+1\) の 上側 だ.
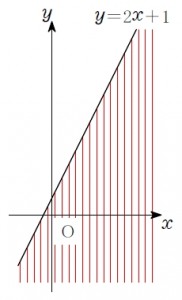
逆に, 不等式 \(y\color{red}{<}2x+1\) の表す領域は,
直線 \(y=2x+1\) より小さい \(y\) 座標をもつ点全体の集まりになり,
直線 \(y=2x+1\) の 下側 だ.
同じように考えて,
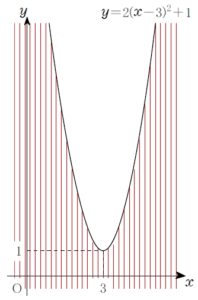
不等式 \(y\color{red}{>}2(x-3)^2+1\) は
放物線 \(y=2(x-3)^2+1\) の上側 領域を表す.
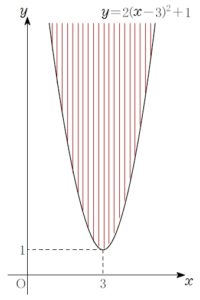
不等式 \(y\color{red}{<}2(x-3)^2+1\) は
放物線 \(y=2(x-3)^2+1\) の下側 領域を表す.
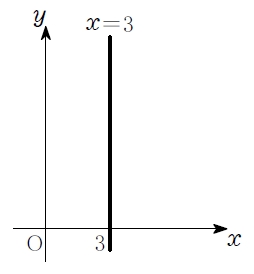
さらに, 方程式 \(x=3\) のグラフは,
「\(x\) 座標が \(3\) である点の集まり」 と考えると,
\(x\) 軸に垂直な直線だとわかるね.
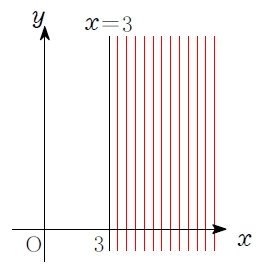
すると, 不等式 \(x\color{red}{>}3\) の表す領域は,
「\(x\) 座標が \(3\) より大きい点の集まり」 だから,
直線 \(x=3\) の 右側.
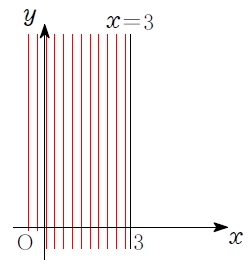
また, 不等式 \(x\color{red}{<}3\) の表す領域は,
「\(x\) 座標が \(3\) より小さい点の集まり」 だから,
直線 \(x=3\) の 左側.
■連立不等式の表す領域■
「連立」 とは 「同時に成り立つ」 ことだ.
連立不等式
\begin{equation}
\left \{
\begin{array}{l}
y<2x+1\ \ \cdots\cdots\ ① \\
y>2(x-3)^2+1\ \ \cdots\cdots\ ②
\end{array}
\right.
\end{equation}
の表す領域は, ① と ② を同時に満たす点 \((x,\ y)\) の集まりということになるね.
つまり, ① と ② の \(\large{共通部分}\) だ.
さらにいうと, 直線 \(y=2x+1\) の下側, かつ, 放物線 \(y=2(x-3)^2+1\) の上側.
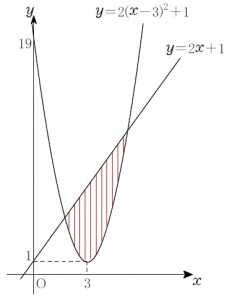
★Point 4 <領域>★
\(y\color{red}{>}\) は上側, \(y\color{red}{<}\) は下側
\(x\color{red}{>}\) は右側, \(x\color{red}{<}\) は左側
連立不等式なら各領域の \(\large{共通部分}\).
●例題 <グラフと領域>●
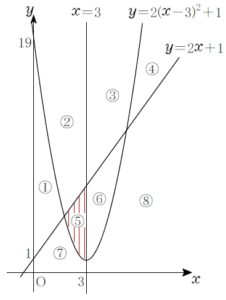
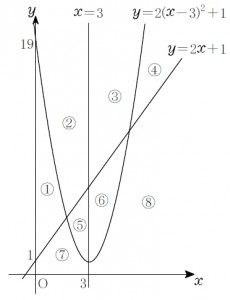
座標平面が, \(3\) 式
\(y=2x+1\), \(y=2(x-3)^2+1\), \(x=3\)
で表されるグラフにより \(8\) つの領域に分けられている.
次の連立不等式で表される領域は図の ① ~ ⑧ のどれか.
\begin{equation}
\left \{
\begin{array}{l}
y<2x+1 \\
y>2(x-3)^2+1 \\ x<3
\end{array}
\right.
\end{equation}
●解答●
\(y<2x+1\) を満たす点 \((x,\ y)\) の集まりは, 直線 \(y=2x+1\) の下側の ⑤, ⑥, ⑦, ⑧.
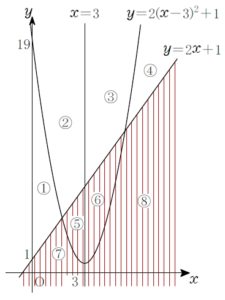
このうち \(y>2(x-3)^2+1\) も満たすのは, 放物線 \(y=2(x-3)^2\) の上側の ⑤, ⑥.

このうち \(x<3\) も満たすのは, 直線 \(x=3\) の左側の ⑤.