\(1\) 仕事 (ひとしごと) 終えるっていうじゃない.
● 仕事算って? ●
ある仕事を終えるのにかかる時間に関する問題.
そのスピンオフが 「水槽算」.
仕事をするのは人間とは限らず, 水を出し入れする管であることも.
解法のポイントは,
① 全体量を \(\color{red}{1}\) とする
② 単位時間あたりで考える
単位時間とは 「\(1\) のつく時間」 のこと.
\(1\) 秒, \(1\) 分, \(1\) 時間, \(1\) 日, \(\cdots\)
\(1\) \(1\) うるさいってか.
■ 例題 1 <仕事算> ■
ある仕事をするのに, A が \(1\) 人ですれば \(6\) 時間かかり, B が \(1\) 人ですれば \(3\) 時間かかる.
A, B の \(2\) 人が同時にすると何時間かかるか.
■ 解答 ■
この仕事の 全体量を \(1\) とする.
A は \(6\) 時間で \(1\) の仕事をするので,
\(1\) 時間あたり \(\displaystyle\color{blue}{\frac{1}{6}}\) の仕事をする.
B は \(3\) 時間で \(1\) の仕事をするので,
\(1\) 時間あたり \(\displaystyle\color{red}{\frac{1}{3}}\) の仕事をする.
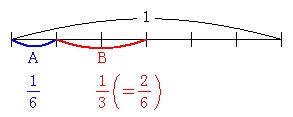
A と B の \(2\) 人では, \(1\) 時間あたり
\(\displaystyle\color{blue}{\frac{1}{6}}+\color{red}{\frac{1}{3}}=\color{blue}{\frac{1}{6}}+\color{red}{\frac{2}{6}}=\frac{3}{6}=\frac{1}{2}\)
の仕事をする.
全体量 \(1\) の仕事をするのに \(2\) 時間かかる.
答 \(2\) 時間
SPONSORED LINK
■ 例題 2 <水槽算> ■
ある水槽を水でいっぱいにするのに, A 管 \(1\) 本で給水すると \(12\) 分, B 管 \(1\) 本で給水すると \(6\) 分かかる.
A 管 \(2\) 本と B 管 \(1\) 本の計 \(3\) 本で同時に給水すると何分かかるか.
■ 解答 ■
水槽に入る水の 全体量を \(1\) とする.
A 管は \(1\) 分あたり \(\displaystyle\color{blue}{\frac{1}{12}}\)
B 管は \(1\) 分あたり \(\displaystyle\color{red}{\frac{1}{6}}\)
の給水をする.
A 管 \(2\) 本と B 管 \(1\) 本の計 \(3\) 本では, \(1\) 分あたり
\(\displaystyle\color{blue}{\frac{1}{12}}\times2+\color{red}{\frac{1}{6}}=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}\)
の給水をする.
全体量 \(1\) を給水するのに \(3\) 分かかる.
答 \(3\) 分