● 推移比率って? ●
ある場所から他の場所へ移る人や物の割合.
移った数を式で表す問題が出題される.
参考書では 「物の流れ (経路・矢印) と比率」 って書いてあることがあるよ.
● 移った数の求め方 ●
\(\rm A\) 駅の利用客 \(100\) 人がいて, その \(\color{red}{3}\) 割 (\(30\%\)) が \(\rm B\) 駅へ移動したとしよう.

移動した人数は
\(100\color{red}{\times0.3}=30\ [人]\)
だね.

\(\rm A\) 駅にいた人数 \(100\) を \(A\), \(\rm B\) 駅へ移った人数 \(30\) を \(B\), 移った比率 \(\color{red}{0.3}\) を \(\color{red}{p}\) で表すと,
\(A \color{red}{\times p}=B\)
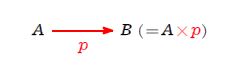
記号 「\(\times\)」 を省略して,
\(B=\color{red}{p}A\)
と表される.
\(\large\color{red}{(移った数)=(移った比率)\times (もとの数)}\)
ということだ.
● 合流地点では足し算 ●
では, \(\rm A\) 駅から \(\rm C\) 駅へ移った比率を \(\color{blue}{p}\),
\(\rm B\) 駅から \(\rm C\) 駅へ移った比率を \(\color{magenta}{q}\) とすると,
\(\rm C\) 駅へ移った人数の合計 \(C\) はどう表されるだろう?
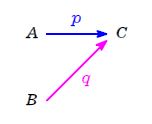
もちろん, \(\rm A\) 駅から来た \(\color{blue}{p}A\ [人]\) と \(\rm B\) 駅から来た \(\color{magenta}{q}B\ [人]\) の 和 で,
\(C=\color{blue}{p}A\color{red}{+}\color{magenta}{q}B\ [人]\)
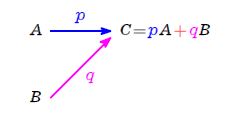
そう,
\(\large\color{red}{合流地点では足し算}\)
だね!
● ゴールから逆にたどって立式, 代入 ●
\(\rm A\) 駅から \(\rm B\) 駅へ移った比率が \(\color{blue}{p}\),
そのうち \(\rm C\) 駅へ移った比率が \(\color{magenta}{q}\) である場合を考えよう.
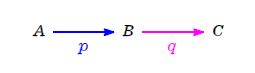
まず, ゴール \(\rm C\) 駅について式をかこう.
\(\rm B\) 駅から \(\color{magenta}{q}\) だけ移っているので,
\(C=\color{magenta}{q}B\) \(\cdots\cdots\) ①

さらに, ゴール \(\rm C\) 駅から \(1\) つ さかのぼった \(\rm B\) 駅についての式を求める.
\(\rm A\) 駅から \(\color{blue}{p}\) だけ移っているので,
\(B=\color{blue}{p}A\) \(\cdots\cdots\) ②

② を ① へ代入すると,
\(C=\color{magenta}{q}\color{blue}{p}A=\color{purple}{pq}A\) \(\cdots\cdots\) ③
となり, ゴール \(\rm C\) 駅へ移った人数は, そこから逆算して最終的にはスタート \(\rm A\) 駅の人数で表現できることがわかるね.
ちなみに, \(\color{purple}{pq}\) の部分は \(\rm A\) 駅から \(\rm C\) 駅へ移った比率を表しているよ.

ここで Point は, 中継駅 \(\rm\color{red}{B}\) に関する式 ①, ② を見逃さない こと!
\(C\) の式をすべて求めよという問題の場合,
図を見て即座に ③ のみを考えてしまうと, 答えとして ① を漏らしてしまう可能性がある.
ゴールから \(\color{red}{1}\) つずつ逆にたどって 式を求めていけば, そのような心配はないぞ.
Point <推移比率> ★★★
・ \(\large\color{red}{(移った数)}\) \(\large\color{red}{=(移った比率)\times (もとの数)}\)
・ \(\large\color{red}{合流地点では足し算}\)
・ \(\large\color{red}{ゴールから逆にたどって立式, 代入}\) (式をすべて求める問題)
SPONSORED LINK
■ 例題 ■ <推移比率>
図の \(A\), \(B\), \(C\), \(D\) はある時間帯の \(4\) つの駅 \(\rm A\), \(\rm B\), \(\rm C\), \(\rm D\) の利用客数を表しており, \(\color{blue}{p}\), \(\color{magenta}{q}\), \(\color{green}{r}\) は利用客の各駅間の移動比率を表している.

\((1)\) \(D\) を表す式を, 次の ア ~ オ からすべて選べ.
ア \(\color{green}{r}C\)
イ \(\color{blue}{p}\color{magenta}{q}\color{green}{r}AB\)
ウ \(\color{blue}{p}\color{green}{r}A+\color{magenta}{q}\color{green}{r}B\)
エ \((\color{blue}{p}+\color{magenta}{q}+\color{green}{r})AB\)
オ \(\color{blue}{p}A+\color{magenta}{q}B+\color{green}{r}C\)
\((2)\) \(\color{blue}{p=0.5}\), \(\color{magenta}{q=0.3}\), \(\color{green}{r=0.4}\) のとき, \(\rm A\) から \(\rm D\) への移動比率を求めよ.
■ 解答 ■
\((1)\)
\(C\) のうち \(\color{green}{r}\) だけ \(D\) へ移動しているので,
\(D=\color{green}{r}C\) \(\cdots\cdots\) \((ア)\)

\(A\) のうち \(\color{blue}{p}\) だけ, \(B\) のうち \(\color{magenta}{q}\) だけ \(C\) へ移動しているので,
\(C=\color{blue}{p}A+\color{magenta}{q}B\)

これを \((ア)\) へ代入して,
\(D=\color{green}{r}(\color{blue}{p}A+\color{magenta}{q}B)\)
\(=\color{green}{r}\color{blue}{p}A+\color{green}{r}\color{magenta}{q}B\)
\(=\color{teal}{pr}A+qrB\) \(\cdots\cdots\) \((ウ)\)
答 ア, ウ
\((2)\)
\(A\) のうち \(p\) だけ \(\rm C\) へ移動し, そのうちの \(r\) だけ \(\rm D\) へ移動しているので,
\((1)\) の \((ウ)\) の式の \(\color{teal}{pr}\) の部分が, \(\rm A\) から \(\rm D\) への移動比率を表している.
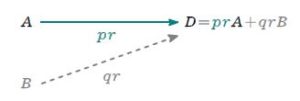
※ 図は \(C\) を省略した形.
\(\color{teal}{pr}=\color{blue}{p}\times \color{green}{r}=\color{blue}{0.5}\times \color{green}{0.4}=0.2\)
答 \(0.2\)
\((2)\) では, \(\color{magenta}{q=0.3}\) は問題に関係ありません.